Disc Graph 1 2 3

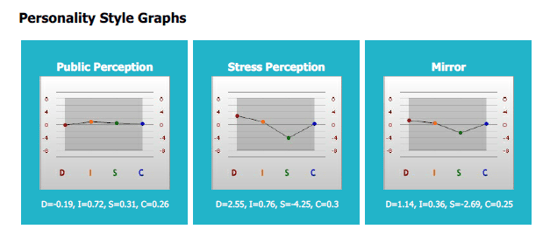
Graph 2 - Natural instinctive behaviour under stress This graph reflects the stored and accepted information from your past and tends to be the most static of the three graphs. Graph 3 - Self-perception This is a summary graph of the earlier two graphs. It is a description of your self-identity and shows your adapted behaviour. Graph 2: These are your 'Least' responses for each of the four scales. Graph 3: This graph is the result of combining your 'Most' choices with your 'Least' choices and is used to determine your highest DiSC dimension, Intensity Index scores, and Classical Profile Pattern. (Graph 3 is automatically included in the Online DiSC Classic 2.0 and DiSC Classic 2 Plus Reports).

1. Disc Graph 1 2 3/4
2. Disc Graph 1 2 3
3. Disc Graph 1 2 3x 1

The volume is going to be equal to the definite integral from negative 1 to 3 of pi times our radius squared dy. So I can write the pi out here- we've done this multiple times- times radius squared- so it's going to be square root of y plus 1 plus 2 squared- that's our radius- times dy. Approach with control. Make more putts. When you have the right discs, your disc golf game can improve quickly. To make the search easier, we've put every Innova disc into one list sortable by Disc Name, Speed, Glide, Turn, Fade, and Abbreviation. 35,489 royalty free Disc clip art images on GoGraph. Download high quality royalty free Disc clip art from our collection of 41,940,205 royalty free clip art graphics.

Abstract

For each (k, k_1, k_2, k_3, k_4 in mathbb{N}), we will denote by (P_k big((k_1, k_2), (k_3, k_4)big)) a tree of (k+k_1+k_2+k_3+k_4+1) vertices with the degree sequence ((1,1,1,1,2,2,2,dots,2,3,3)). Let (alpha_{k_1}, beta_{k_2}, sigma_{k_3}), and (delta_{k_4}) be all four endpoints of the graph. Let the distance between both vertices of degree 3 be equal to (k). A subset (S) of vertices of a graph (P_k big((k_1, k_2), (k_3, k_4)big)) is a dominating set of (P_k big((k_1, k_2), (k_3, k_4)big)) if every vertex in (Vbig(P_k big((k_1, k_2), (k_3, k_4)big)big)-S) is adjacent to some vertex in (S). We investigate the dominating set of minimum cardinality of a graph (P_k big((k_1, k_2), (k_3, k_4)big)) to obtain the domination number of this graph. Finally, we determine an upper bound on the domination number of a graph (P_k big((k_1, k_2), (k_3, k_4)big)).

Keywords

Disc Graph 1 2 3/4

References

S. Alikhani, Y. H. Peng and K. A. M. Atan, On the domination number of some graphs, Int. Math. Forum 3(38) (2008), 1879 – 1884.

M. M. Bacolod and M. P. Baldado Jr., Domination number of the acquaint vertex gluing of graphs, Appl. Math. Sci. 8(161) (2014), 8029 – 8036.

G. Chartrand and P. Zhang, Introduction to Graph Theory, International edition, McGraw-Hill, 361 – 368 (2005).

T. T. Chelvam and G. Kalaimurugan, Bounds for domination parameters in Cayley graphs on dihedral group, Open J. > observer_ download free. Discrete Math. 2(1) (2012), 5 – 10, DOI: 10.4236/ojdm.2012.21002.

A. Frendrup, M. A. Henning, B. Randerath and P. D. Vestergaard, An upper bound on the domination number of a graph with minimum degree, Discrete Mathematics 309(2) (2009), 639 – 646, DOI: 10.1016/j.disc.2007.12.080.

T. W. Haynes, S. T. Hedetniemi and P. J. Slater, Fundamentals of Dominations in Graphs, Marcel Dekker, New York (1998).

J. Huang and J. M. Xu, Domination and total domination contraction numbers of graphs, Ars Combinatoria 94 (2010), 431 – 443, URL: http://staff.ustc.edu.cn/~xujm/201004.pdf.

A. V. Kostochka and C. Stocker, A new bound on the domination number of connected cubic graph, Siberian Elect. Math. Reports 6 (2009), 465 – 504, URL: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.224.9130. Exposure x5 5 2 1 211 0.

A. V. Kostochka and B. Coolmuster android assistant 4 3 51. Y. Stodolsky, An upper bound on the domination number of n-vertex connected cubic graphs, Discrete Math. 309 (2009), 1142 – 1162, DOI: 10.1016/j.disc.2007.12.009.

N. Murugesan and D. S. Nair, The domination and independence of some cubic bipartite graphs, Int. J. Contemp. Math. Sciences 6 (2011), 611 – 618.

N. Nupo and S. Panma, Domination in Cayley digraphs of rectangular groups, in Proceedings of International Conference on Science & Technology, Bangkok (2014).

R. Wilson, Introduction to Graph Theory, 4th edition, Addison Wesley Longman Limited, England (1996).

Disc Graph 1 2 3

Keywords

Disc Graph 1 2 3/4

References

S. Alikhani, Y. H. Peng and K. A. M. Atan, On the domination number of some graphs, Int. Math. Forum 3(38) (2008), 1879 – 1884.

M. M. Bacolod and M. P. Baldado Jr., Domination number of the acquaint vertex gluing of graphs, Appl. Math. Sci. 8(161) (2014), 8029 – 8036.

G. Chartrand and P. Zhang, Introduction to Graph Theory, International edition, McGraw-Hill, 361 – 368 (2005).

T. T. Chelvam and G. Kalaimurugan, Bounds for domination parameters in Cayley graphs on dihedral group, Open J. > observer_ download free. Discrete Math. 2(1) (2012), 5 – 10, DOI: 10.4236/ojdm.2012.21002.

A. Frendrup, M. A. Henning, B. Randerath and P. D. Vestergaard, An upper bound on the domination number of a graph with minimum degree, Discrete Mathematics 309(2) (2009), 639 – 646, DOI: 10.1016/j.disc.2007.12.080.

T. W. Haynes, S. T. Hedetniemi and P. J. Slater, Fundamentals of Dominations in Graphs, Marcel Dekker, New York (1998).

J. Huang and J. M. Xu, Domination and total domination contraction numbers of graphs, Ars Combinatoria 94 (2010), 431 – 443, URL: http://staff.ustc.edu.cn/~xujm/201004.pdf.

A. V. Kostochka and C. Stocker, A new bound on the domination number of connected cubic graph, Siberian Elect. Math. Reports 6 (2009), 465 – 504, URL: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.224.9130. Exposure x5 5 2 1 211 0.

A. V. Kostochka and B. Coolmuster android assistant 4 3 51. Y. Stodolsky, An upper bound on the domination number of n-vertex connected cubic graphs, Discrete Math. 309 (2009), 1142 – 1162, DOI: 10.1016/j.disc.2007.12.009.

N. Murugesan and D. S. Nair, The domination and independence of some cubic bipartite graphs, Int. J. Contemp. Math. Sciences 6 (2011), 611 – 618.

N. Nupo and S. Panma, Domination in Cayley digraphs of rectangular groups, in Proceedings of International Conference on Science & Technology, Bangkok (2014).

R. Wilson, Introduction to Graph Theory, 4th edition, Addison Wesley Longman Limited, England (1996).

Disc Graph 1 2 3

Refbacks

• There are currently no refbacks.

Disc Graph 1 2 3x 1